
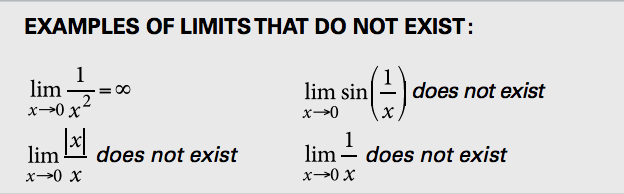
Also, we learned about how to determine the limits of composite function and how to determine limits with comparison. In this article, we discovered the different indeterminate forms and how to avoid them and calculate the limits using L’Hôpital’s rule, with examples of the various cases. We know that for every from, we have, and then for every from, we have Remarque: these three theorems can be extended to the two cases for the limit when tends to or a real number. Suppose and two functions and a real number if we have, and if for big enough we have then. Let’s consider the function defined on as Suppose, , and three functions, and a real number if we have and and if for big enough we have then. We notice that the function is a composite of two functions, precisely is a composite of the functions and in this order ( ), where Let’s consider the function defined on the domain asĪnd we want to determine the limit of the function when tends to, i.e., If the limit of the function when tends to is, and the limit of the function when tend to is then the limit of the function when tends to is. Let, and represent real numbers or or, and let, , and be functions that verify. Now we calculate the limit of the exponent using L’Hôpital’s rule: This limit gives us the indeterminate form, to use the L’Hôpital’s rule we need to re-write the expression as follow: This limit gives us the form, to avoid it and be able to apply L’Hôpital’s rule we need to re-write the expression as follow:
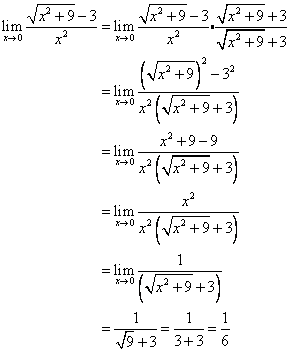
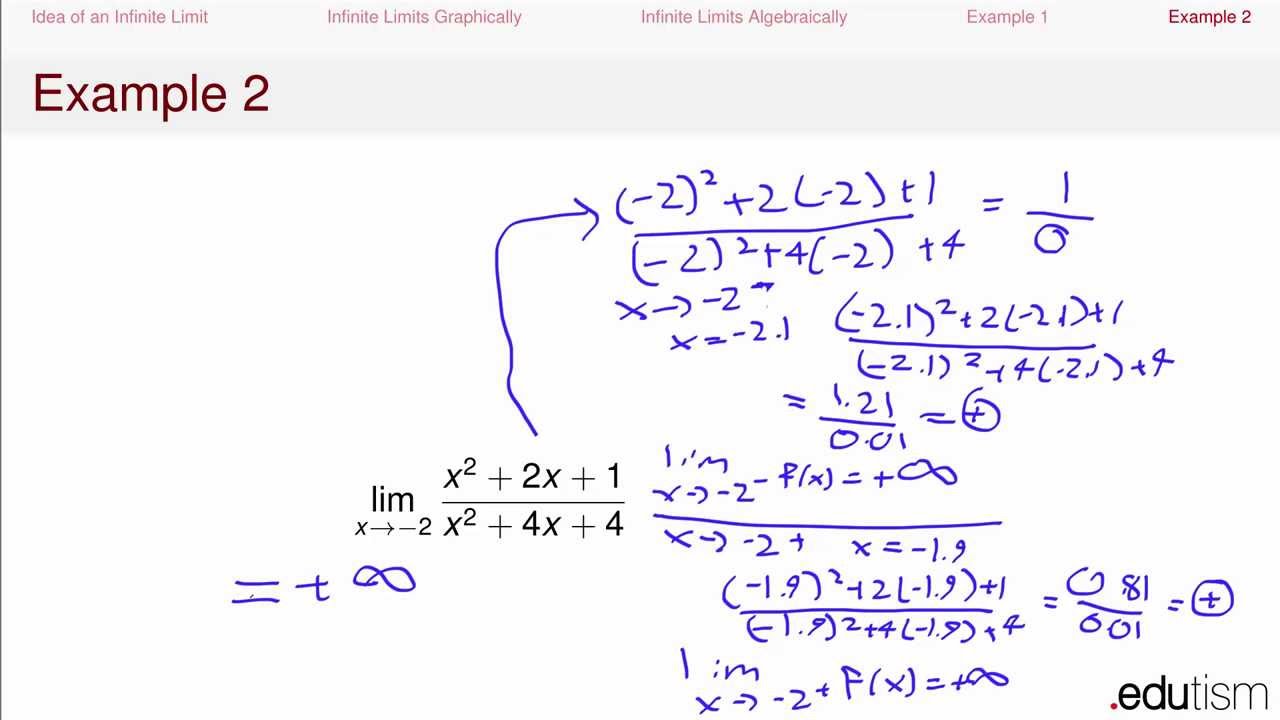
Now by applying the L’Hôpital’s rule twice (because we get the indeterminate form after the first time) we get: Now the limit of the expression gives us the form. This limit gives us the form, to apply the L’Hôpital’s rule we need to re-write the expression, in this case, all we need to do is combine the two fractions as follow: This limit gives us the form, to apply the L’Hôpital’s rule we need to take a few steps as follow:īy applying the natural logarithm, we get:Īnd from what we got before we can solve the problem as follow: Now by computing the limit we have the form, therefore we can apply L’Hôpital’s rule and we get: Here we have the indeterminate form, to use L’Hôpital’s rule we re-write the expression as follow: Let’s see some examples of how to do that!!! In this case, after we get the derivatives of the quotient, we still get the indeterminate form of the type so we apply L’Hôpital’s Rule again, and therefore we get:įor other Indeterminate forms, we have to do some transformation on the expression to bring it to one of the two forms that L’Hôpital’s rule solves. Then we calculate the limit of the derivatives of the quotient of and, i.e., Where is a real number or infinity, and if we have one of the following cases:
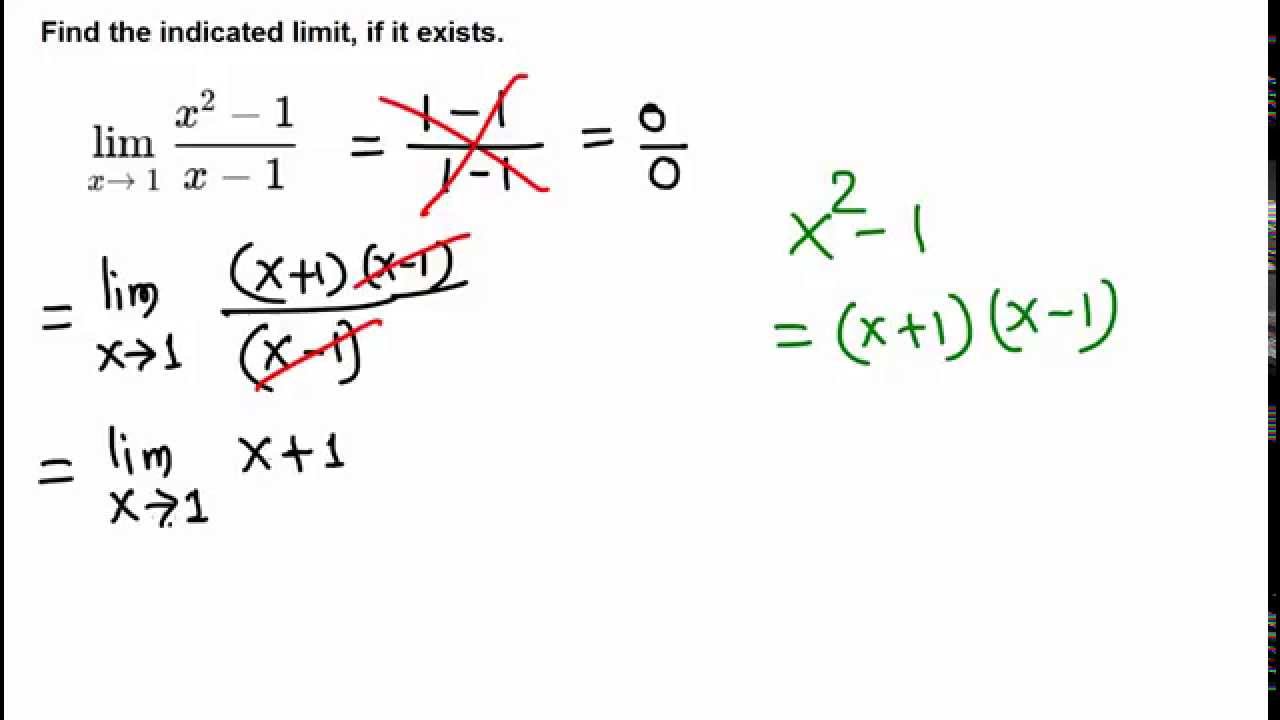
L’Hôpital’s rule is a method used to evaluate limits when we have the case of a quotient of two functions giving us the indeterminate form of the type or.
L’Hôpital’s rule and how to solve indeterminate forms Here are some examples to illustrate each of these indeterminate cases: In total there is seven indeterminate forms, here they are: We call an indeterminate form, when computing limits the case when we get an expression that we cannot determine the limit. While studying calculus or other branches of mathematics we may need to find the limits of a function, a sequence, or an expression, and in doing so we stumble on a situation where we cannot determine the limits, in this article we will learn about the different indeterminate forms and how to work around them in order to find the limits we are looking for.


 0 kommentar(er)
0 kommentar(er)
